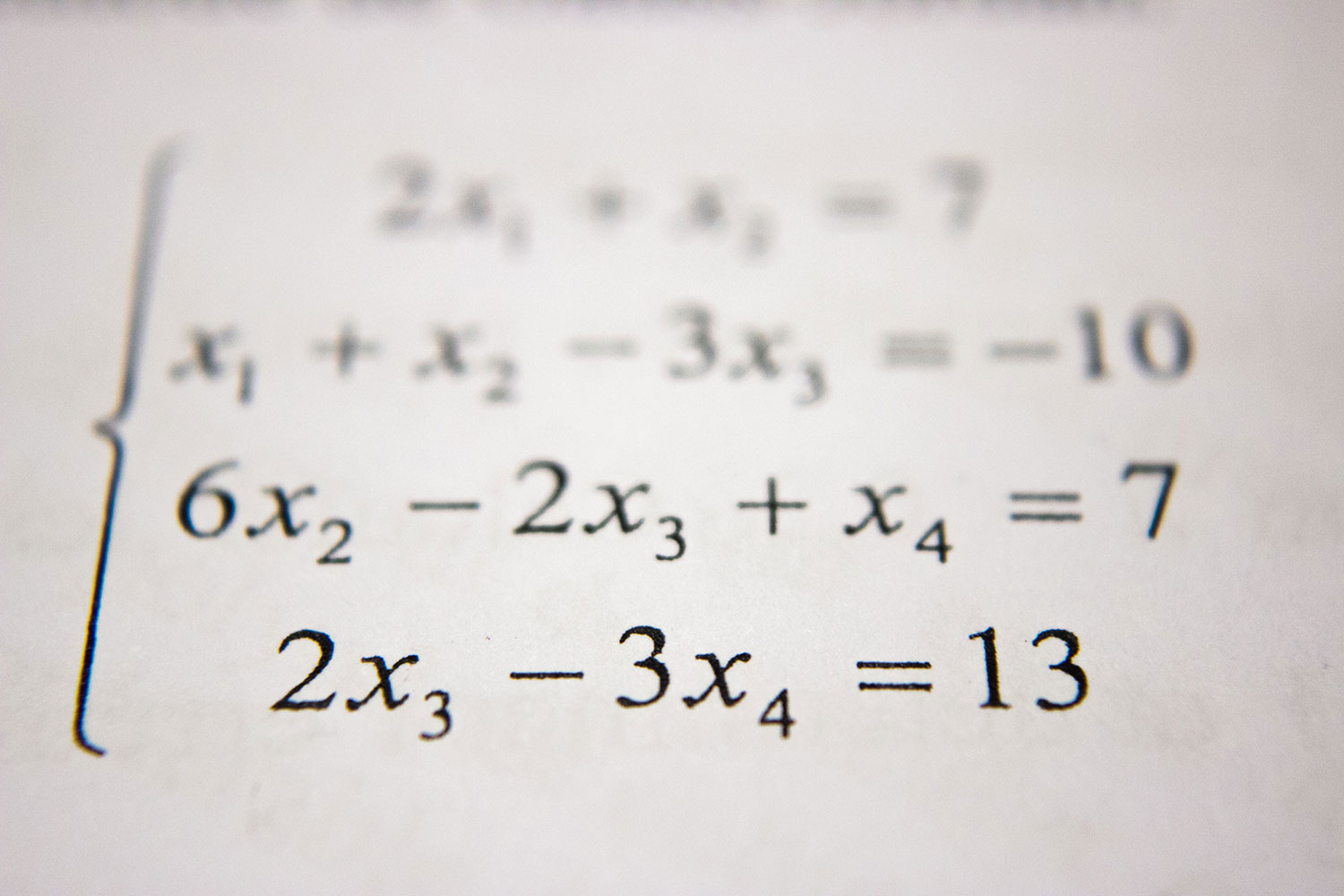古典音樂與數學
知名古希臘數學家暨哲學家畢達哥拉斯(Pythagoras)是有記載以來最早提出數學與音樂連結的人物之一。他發現了振動弦的音高變化與長度之間的關係。如果兩條弦的長度比是2:3,那麼兩弦音程就會是完全五度(例如D—A)。他的理論後來被柏拉圖在《論靈魂》加以深入討論與發展。
不搞得太複雜的話,我們也能在關於節奏分割的兩個話題上找到這種連結。如果想一下傳統記譜法,我們在譜號旁邊首先會看到的東西是「拍號」。(圖1)
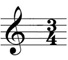
▲圖1:拍號
這兩個數字告訴演奏者這首曲子的每個小節如何分割。在3/4拍的例子中,每個小節最多三個四分音符。這個小節能包含各種不同的時值變化,只要加起來是三個四分音符(亦即三個一拍)就行。於是數學又扯上關係了。
接著就能說到音符時值的各種分割,彼此之間的關係本身就能被視為數學關係(圖2)
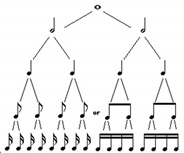
▲圖2:音符的數學關係
圖2描繪了全音符(最上方)被漸次分割成更小的時值,每次都是一分為二。
節拍器記號也能與數學有關。這種音樂指示法告訴演奏者樂曲的準確速度,而不是以詞語描述。作曲家往往會寫「快板」、「行板」、「慢板」來指示他們作品的速度與性格,但這些詞語並不能傳達樂曲的實際速度。節拍器記號是音樂速度的數字表達形式。如果作曲家希望一首樂曲每秒演奏一個四分音符,那麼他就能把節拍器記號寫成「四分音符=60」(圖3)
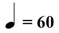
▲圖3:四分音符=60
以此類推,「四分音符=120」就是兩倍快;「四分音符=180」則是三倍快。
阿諾.荀貝格(Arnold Schoenberg)發明了一種全然革命性的作曲技法,世稱「序列主義」(Serialism)。荀貝格創造這種作曲工具,以打破傳統調性作曲系統的桎梏。在荀貝格的取徑當中,他准許半音階上的每個音有著一樣的重要性,並完全捨棄調性概念。他的學生,阿班.貝爾格(Alban Berg)與安東.魏本(Anton Webern)也各自以大相逕庭的風格採取這種作曲技法,但兩人都基於人稱「音列」(tone-rows)的技巧。
音列構成作品的根基,提供音樂素材。建構音列,根據荀貝格的原則,就是在半音階的每個音出現之前不重複使用同樣音高。這也就是說,半音階裡的12個音高在音列當中出現機會均等。
從這些概念出發,你就能開始了解作曲過程中的數學會是什麼樣子。後來的作曲家,像是布列茲(Pierre Boulez)、卡特(Elliott Carter)、許托克豪森(Karlheinz Stockhausen),以及某部份的梅湘(Olivier Messiaen),他們都以序列手法決定音樂中的幾乎所有面向,從音高、節奏、乃至於作品整體結構。這種手法為作品帶來的效果必須實際聆聽。對很多人來說,這種讓音樂更加數學化的發展,有點走得太前面,某種意義上來說又幾乎抹除了讓所有人親近作曲成果的可能性。
(布列茲在雙鋼琴作品《結構》中使用的整體序列手法,詳細分析可見《MUZIK古典月刊》2016年7月號第110期。)
在希臘作曲家協納基斯(Iannis Xenakis)的作品當中,他直接使用隨機數學(stochastic mathematics)作曲。他宣稱每個對數學概念有基本掌握的人都能使用這種技法,不過我覺得他好像低估了這項任務的複雜程度。對我來說,協納基斯產出了很多重要作品,其中的音樂性並未受背後的作曲程序所掩蓋。他其中一件劃時代的作品是1954年的《轉移》Metastaseis),使用了十二音技法以及費氏數列來探討愛因斯坦的時間觀。這首音樂以一種開放坦承的方式與數學產生直接連結,就我所知是前無古人的。成果令人屏息,美得獨一無二。